Mata Kuliah: Machine Learning
Logistic Regression
Pendahuluan
- Dalam supervised learning untuk klasifikasi, kita ingin memprediksi kelas dari data baru berdasarkan data latih. Kelas adalah variabel kategorik (diskrit). Misalnya, spam atau not spam, sakit atau sehat, bangkrut atau tidak bangkrut, dll.
- Regresi logistik adalah salah satu algoritme yang paling umum digunakan untuk klasifikasi biner.
- Regresi logistik memodelkan probability kelas dengan menekan kombinasi linear fitur melalui fungsi sigmoid.
- Cocok untuk klasifikasi biner dan dapat diperluas ke multikelas menggunakan softmax regression.
- Algoritma ML ini lebih interpretatif dibandingkan algoritma lain seperti SVM, decion tree, dan neural networks.
- odds ratio digunakan untuk interpretasi koefisien regresi logistik.
Model Umum Regresi Logistik
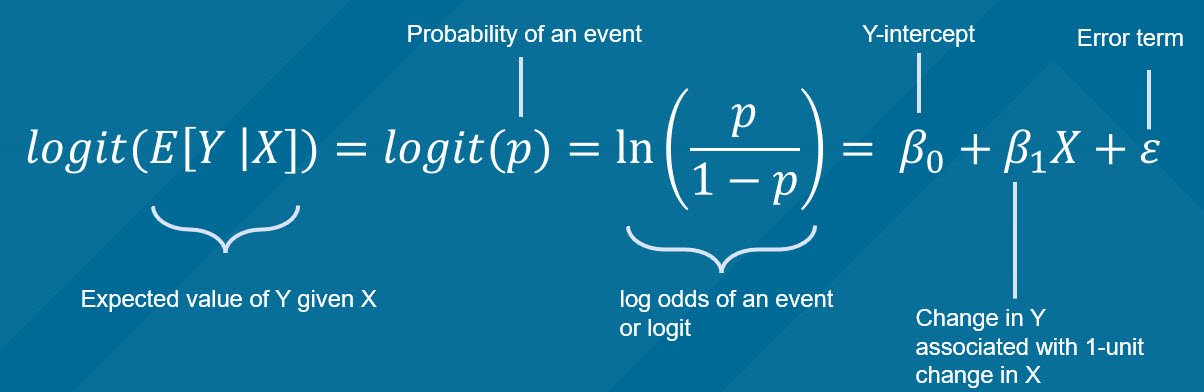
Dalam statistik, kita sering menggunakan model regresi untuk memprediksi variabel dependen (target) berdasarkan satu atau lebih variabel independen (fitur). Model regresi logistik digunakan ketika variabel dependen bersifat kategorik, khususnya untuk klasifikasi biner.
logit(p) adalah fungsi log-odds yang menghubungkan probabilitas kejadian suatu peristiwa dengan model regresi linear. Fungsi ini digunakan untuk memodelkan hubungan antara variabel dependen dan independen dalam regresi logistik.
Interpretabilitas pada Model Umum
Interpretasi koefisien regresi logistik dapat dilakukan dengan menggunakan odds ratio (OR). OR adalah rasio peluang kejadian suatu peristiwa dibandingkan dengan peluang tidak terjadinya peristiwa tersebut. Dalam konteks regresi logistik, OR dapat dihitung sebagai eksponensial dari koefisien regresi.
\[ OR = \exp(\beta_j) \]
- \(\beta_j\) → perubahan log‑odds per kenaikan satu unit \(x_j\).
- Odds Ratio (OR): \(\exp(\beta_j)\) → OR > 1 meningkatkan peluang kejadian, OR < 1 menurunkannya.
- Misalnya, jika \(\beta_j = 0.5\), maka OR = \(\exp(0.5) \approx 1.65\). Ini berarti bahwa untuk setiap kenaikan satu unit pada \(x_j\), peluang kejadian peristiwa meningkat sekitar 65%. Atau misalnya jika \(x_j\) adalah gender, maka peluang seorang pria (\(x_j\) = 1) dibandingkan wanita (\(x_j\) = 0) adalah 1.65 kali lebih besar untuk mengalami peristiwa tersebut.
Fungsi Likelihood & Estimasi
Model regresi logistik tidak lagi menggunakan OLS (Ordinary Least Squares) untuk estimasi parameter, tetapi menggunakan Maximum Likelihood Estimation (MLE). MLE adalah metode statistik yang digunakan untuk memperkirakan parameter model dengan memaksimalkan fungsi likelihood.
Log-Likelihood
\[ \ell(\boldsymbol\beta) = \sum_{i=1}^{N} \left[\, y_i \log \hat{p}_i + (1 - y_i)\log (1 - \hat{p}_i) \right] \]
Estimasi Maksimum Likelihood
Koefisien \(\boldsymbol\beta\) diestimasi dengan memaksimalkan log-likelihood menggunakan metode numerik seperti Newton-Raphson atau iterasi Fisher scoring.
Fungsi Sigmoid
Dalam environmen ML, kita sering menggunakan fungsi aktivasi untuk mengubah output dari model menjadi probabilitas. Interpretabikitas model kadang tidak terlalu penting, karena fokus pada kinerja akurasi model.
Dalam package scikit-learn, fungsi yang digunakan untuk klasifikasi adalah LogisticRegression yang menggunakan fungsi sigmoid. Fungsi sigmoid adalah fungsi aktivasi yang mengubah output model menjadi probabilitas antara 0 dan 1.
\[ \sigma(z) = \frac{1}{1 + e^{-z}} \]
Di mana \(z\) adalah kombinasi linear dari variabel independen:
\[ z = \beta_0 + \beta_1x_1 + \dots + \beta_p x_p \]
Model Regresi Logistik
Prediksi probabilitas kejadian dalam diturunkan dari fungsi sigmoid:
\[ \hat{p}_i = \sigma\!\bigl(\mathbf{x}_i^\top \boldsymbol\beta\bigr) \]
Keputusan biner:
\(j_i = 1\) bila \(\hat{p}_i \ge \tau\) (default \(\tau = 0.5\)).
Regularisasi
Dalam scikit-learn, kita dapat menggunakan parameter C untuk mengatur kekuatan regulasi. Semakin kecil nilai C, semakin kuat regulasi yang diterapkan pada model. Terdapat dua jenis regulasi yang umum digunakan dalam regresi logistik:
L2 (Ridge):
\[ \ell_{\text{reg}} = \ell - \lambda \lVert \boldsymbol\beta \rVert_2^2 \]
L1 (Lasso):
\[ \ell_{\text{reg}} = \ell - \lambda \lVert \boldsymbol\beta \rVert_1 \]
Di Scikit‑Learn, parameter regulasi dinyatakan dengan C = 1/\(\lambda\)
Multiclass: Softmax Regression
Untuk \(K\) kategori, misalnya \(K = 3\), kita dapat menggunakan softmax regression untuk memodelkan probabilitas kelas. Fungsi softmax mengubah output model menjadi probabilitas yang dijumlahkan menjadi 1. Kasus multiclass misalnya adalah klasifikasi tingkat kepuasan pelanggan: sangat tidak puas, tidak puas, netral, puas, sangat puas.
\[ P(y = c \mid \mathbf x) = \frac{\exp\bigl(\boldsymbol\beta_c^\top \mathbf x\bigr)} {\displaystyle\sum_{k=1}^{K} \exp\bigl(\boldsymbol\beta_k^\top \mathbf x\bigr)} \]
Fungsi log-likelihood: multiclass cross‑entropy:
\[ \ell = \sum_{i=1}^{N} \sum_{k=1}^{K} y_{ik} \log P(y = k \mid \mathbf x_i) \]
Evaluasi Model

- Confusion Matrix, Accuracy
- Precision, Recall, F1‑Score
- ROC‑AUC dan Log‑loss untuk evaluasi probabilistik
Implementasi Scikit‑Learn
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
X, y = load_breast_cancer(return_X_y=True)
log_reg = LogisticRegression(
penalty='l2', # 'l1', 'elasticnet', None
solver='lbfgs', # 'liblinear', 'saga', ...
max_iter=1000,
C=1.0, # 1/λ
random_state=42
)
print(cross_val_score(log_reg, X, y, cv=10).mean())Solver adalah algoritme optimasi yang digunakan untuk memperbarui koefisien model selama pelatihan.
Penjelasan masing-masing solver:
liblinear: Algoritme optimasi berbasis koordinat yang efisien untuk dataset kecil hingga menengah. Cocok untuk regulasi L1 dan L2.lbfgs: Algoritme optimasi berbasis kuasi-Newton yang efisien untuk dataset besar. Cocok untuk regulasi L2. Untuk lebih jelas dapat dilihat pada scikit-learn documentation.
Hyper‑parameter Kunci
| Parameter | Fungsi | Efek |
|---|---|---|
penalty |
Jenis regulasi ('l2','l1',…) |
Kendali overfitting |
C |
\(1/\lambda\) (≥ 0) | Bias–variance trade‑off |
solver |
Algoritme optimasi | Dukungan regulasi bervariasi |
max_iter |
Iterasi maksimum | Konvergensi |
class_weight |
Bobot kelas | Penanganan data imbalanced |
Materi Tambahan
- Video: StatQuest – Logistic Regression Explained
- Bab interaktif: D2L – Softmax Regression
