Mata Kuliah: Machine Learning
Regresi Linier dan Teknik Seleksi Peubah: Shrinkage Methods (Ridge, Lasso, Elastic Net)
Review
Model Selection: Subset vs Shrinkage
- Subset Selection
- Best-Subset Selection
- Forward-Stepwise Selection
- Backward-Stepwise Selection
- Best-Subset Selection
- Shrinkage Methods
- Ridge Regression
- Lasso (Least Absolute Shrinkage and Selection Operator)
- Elastic Net
- Ridge Regression
Shrinkage Methods
Logika Dasar Metode Penyusutan Peubah (Shrinkage Methods)
- Metode kuadrat terkecil biasa (ordinary least squares) dapat berkinerja kurang optimal, terutama saat terdapat banyak peubah \(X\), atau ketika jumlah peubah (\(p\)) melebihi jumlah observasi (\(n\)), atau setidaknya mendekati (\(p \approx n\)).
- Alternatifnya adalah dengan menerapkan penalti (penalized), yang memungkinkan dilakukannya penyusutan (shrinkage) peubah, atau yang dikenal juga dengan regularisasi (regularization).
- Dampak dari penerapan penalti ini adalah menyusutkan nilai koefisien (beberapa bisa menjadi nol), yang juga membantu mengurangi permasalahan multikolinieritas. Koefisien yang sangat kecil dapat “dibuang” (dikurangi pengaruhnya) dengan metode tertentu.
- Dalam metode penyusutan, ditambahkan parameter \(\lambda\) yang mengendalikan tingkat penyusutan.
- Terdapat tiga metode penalti utama: ridge regression, lasso, dan elastic net.
Teknis Penyusutan Peubah
\[ Y = \beta_0 + \beta_1 X_1 + \ldots + \beta_p X_p + \epsilon \]
- Metode ini memasukkan semua peubah bebas \(X_i\) (\(i = 1, 2, \ldots, p\)).
- Namun penduga koefisien \(X_i\) (\(\beta_1, \beta_2, \ldots, \beta_p\)) disusutkan menuju nol.
- Jika, misalnya, \(\beta_k\) nilainya mendekati nol atau sama dengan nol, maka hal ini setara dengan mengeliminasi peubah \(X_k\) dari model.
Subset vs Shrinkage
- Dengan mempertahankan sebagian peubah (predictors) dan membuang sisanya, metode subset selection menghasilkan model yang relatif lebih mudah diinterpretasikan dan berpotensi memiliki galat prediksi yang lebih rendah dibandingkan model penuh.
- Namun, karena proses ini bersifat diskrit—variabel dipilih atau tidak dipilih sama sekali—sering kali metode ini memiliki varians yang tinggi, sehingga belum tentu menurunkan galat prediksi model penuh.
- Metode shrinkage bersifat lebih kontinu dan umumnya tidak terlalu terpengaruh oleh variabilitas yang tinggi.
Ilustrasi Shrinkage Methods

Ridge Regression
Di scikit-learn Python, kita dapat menggunakan Ridge atau dikenal sebagai L2 regularization.
\[ \min_{\beta} \bigl\{\;\|y - X\beta\|_{2}^{2} \;+\; \alpha\,\|\beta\|_{2}^{2}\bigr\} \]
- \(\|\beta\|_2^2\) menyatakan penalti L2 (kuadrat norma 2) dari \(\beta\).
- \(\alpha\) adalah parameter regularisasi yang mengatur kekuatan penalti.
Lasso
Di scikit-learn Python, kita dapat menggunakan Lasso atau dikenal sebagai L1 regularization.
\[ \min_{\beta} \bigl\{\;\|y - X\beta\|_{2}^{2} \;+\; \alpha\,\|\beta\|_{1}\bigr\} \]
- \(\|\beta \|_1\) menyatakan penalti L1 (norma 1) dari \(\beta\).
- \(\alpha\) adalah parameter regularisasi yang mengatur seberapa kuat penalti diterapkan.
- Penalti L1 cenderung membuat beberapa koefisien \(\beta_j\) tepat menjadi nol, sehingga melakukan feature selection secara otomatis.
Elastic Net
Di scikit-learn Python, kita dapat menggunakan ElasticNet, yang merupakan gabungan dari Ridge dan Lasso.
\[ \min_{\beta} \Bigl\{\;\|y - X\beta\|_{2}^{2} \;+\; \alpha \bigl[\;\rho\,\|\beta\|_{1} + (1-\rho)\,\|\beta\|_{2}^{2}\bigr]\Bigr\} \]
- Kombinasi penalti L1 dan L2, masing-masing dikendalikan oleh \(\rho\) (disebut
l1_ratiodi scikit-learn) dan \(\alpha\).
- Saat \(\rho = 1\), Elastic Net menjadi Lasso murni; sedangkan \(\rho = 0\) menjadi Ridge.
- Memadukan kelebihan Ridge (stabil terhadap multikolinieritas) dan Lasso (menekan koefisien ke nol).
Mengingat Kembali Norm
Norm adalah fungsi yang mengukur panjang vektor. Dalam konteks ini, kita mengenal dua jenis norm yang sering digunakan dalam regularization:
Norm L2 (Euclidean Norm):
\[ \|x\|_2 := \sqrt{\sum_{i=1}^n x_i^2} \]
Norm L1 ( Manhattan Norm):
\[ \|x\|_1 := \sum_{i=1}^n |x_i| \]
Pemilihan Nilai Parameter \(\alpha\) (Tuning Parameter)
- Sama seperti pendekatan pemilihan subset, diperlukan metode khusus untuk menentukan model terbaik.
- Pada regresi ridge dan LASSO, kita perlu memilih nilai parameter tuning \(\alpha\).
- Cross-validation dapat digunakan untuk mengestimasi galat. Kita membuat sekumpulan (grid) nilai \(\alpha\), lalu menghitung kesalahan prediksi untuk setiap nilai \(\alpha\) tersebut.
- Nilai \(\alpha\) dengan kesalahan cross-validation terkecil kemudian dipilih sebagai parameter terbaik.
- Terakhir, model disesuaikan kembali menggunakan seluruh data yang tersedia dengan nilai \(\alpha\) terpilih.
Pemilihan Nilai Parameter \(\alpha\) (Tuning Parameter)
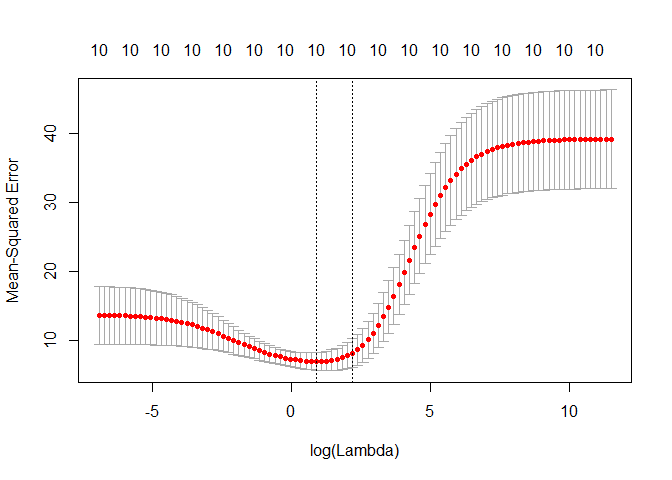
Hubungan LS, Ridge, Lasso, Elastic Net
- Salah satu kelemahan pada regular least squares adalah tidak adanya mekanisme untuk mengatasi overfitting.
- Ridge regression menanggulangi masalah ini dengan “menyusutkan” koefisien parameter tertentu.
- Kelemahan ridge regression adalah tidak mampu melakukan feature selection. Kelemahan ini diatasi oleh LASSO.
- LASSO melangkah lebih jauh dengan memaksa sebagian koefisien parameter menjadi nol, sehingga secara efektif mengeliminasi peubah \(X\) tertentu dari model.
- Elastic Net menggabungkan keunggulan ridge regression dan LASSO sekaligus. Elastic Net lebih fleksibel dan memberi stabilitas.
Code Exercise
Reference
- James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: With Applications in R. New York: Springer.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). New York: Springer Science and Business Media.
- Kusman S. (2021). “Machine Learning: Teori dan Implementasi dengan R”, Penerbit Informatika
- Pacmann Academy
