Mata Kuliah: Machine Learning
Unsupervised Learning: Clustering
Pendahuluan
- Dalam unsupervised learning, kita mencoba menemukan pola atau struktur dalam data tanpa label atau target.
- Clustering adalah salah satu teknik unsupervised learning yang paling umum digunakan untuk mengelompokkan data berdasarkan kemiripan.
- Algoritma clustering mengelompokkan data ke dalam klaster sehingga objek dalam satu klaster lebih mirip satu sama lain daripada dengan objek di klaster lain.
- Clustering digunakan dalam berbagai aplikasi seperti segmentasi pelanggan, analisis gambar, deteksi anomali, pengenalan pola, dll.
- Ada dua jenis metode clustering utama: hierarchical clustering (hirarki) dan non-hierarchical clustering (non-hirarki).
- Metode evaluasi khusus diperlukan karena tidak ada “jawaban benar” untuk membandingkan hasil.
Konsep Dasar Clustering
Dalam clustering, tujuan utama adalah meminimalkan jarak (distance) antar data dalam satu klaster dan memaksimalkan jarak antar klaster. Formula umum yang digunakan adalah:
\[ \text{Minimize} \quad \sum_{i=1}^{K} \sum_{x \in C_i} d(x, \mu_i) \]
di mana:
\(K\) = jumlah klaster
\(C_i\) = klaster ke-\(i\)
\(x\) = data pada klaster \(C_i\)
\(\mu_i\) = pusat (centroid) klaster \(C_i\)
\(d(x, \mu_i)\) = jarak antara \(x\) dan centroid \(\mu_i\) (umumnya Euclidean)
Jenis-Jenis Clustering
Clustering dapat dibagi menjadi dua kategori utama:
- Hierarchical Clustering (Clustering Hirarki):
- Membentuk hirarki klaster yang dapat divisualisasikan sebagai dendogram
- Tidak memerlukan jumlah klaster ditentukan di awal
- Jenis: Agglomerative (bottom-up) dan Divisive (top-down)
- Non-Hierarchical Clustering (Clustering Non-Hirarki):
- Membagi data menjadi sejumlah klaster yang ditentukan di awal
- Metode populer: K-Means, DBSCAN, Gaussian Mixture Models
Hierarchical Clustering
Hierarchical clustering membangun hirarki klaster dalam bentuk pohon (dendogram).
Agglomerative Clustering (Bottom-up):
Dimulai dengan masing-masing titik data sebagai klaster individual
Secara berulang menggabungkan dua klaster terdekat hingga hanya satu klaster tersisa
Proses penggabungan membentuk dendogram
Divisive Clustering (Top-down):
Dimulai dengan semua titik data dalam satu klaster besar
Secara berulang membagi klaster hingga setiap titik data menjadi klaster individual
Jarang digunakan karena kompleksitas komputasi yang tinggi
Metrik Jarak: Euclidean, Manhattan, Cosine, dll.
Metode Linkage: Single, Complete, Average, Ward’s
Dendogram Hierarchical Clustering
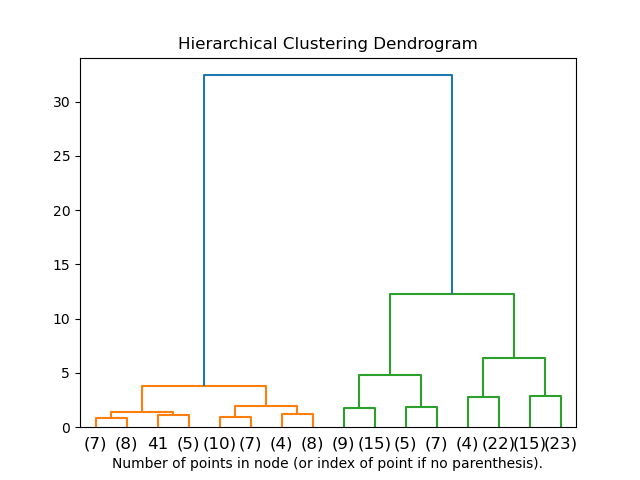
Dendogram menunjukkan:
- Struktur hirarki klaster
- Tingkat kesamaan antara klaster yang digabungkan
- Memungkinkan pemilihan jumlah klaster secara visual
- Sumbu horizontal: objek data
- Sumbu vertikal: jarak/ketidakmiripan
Jumlah klaster dapat dipilih dengan “memotong” dendogram pada tingkat jarak tertentu.
Dendogram Hierarchical Clustering

Metode Linkage
Metode linkage menentukan bagaimana menghitung jarak antar klaster:
| Metode Linkage | Deskripsi | Kelebihan/Kekurangan |
|---|---|---|
| Single linkage | Jarak terpendek antara titik-titik dari dua klaster | Dapat menangani bentuk non-eliptis; rentan terhadap noise |
| Complete linkage | Jarak terjauh antara titik-titik dari dua klaster | Cenderung membentuk klaster yang kompak; sensitif terhadap outlier |
| Average linkage | Rata-rata jarak antara semua pasangan titik | Kompromi antara single dan complete; cukup robust |
| Ward’s method | Meminimalkan peningkatan jumlah kuadrat galat | Cenderung membentuk klaster dengan ukuran yang seimbang |
Metode Linkage

Non-Hierarchical Clustering: K-Means
K-Means adalah algoritma clustering non-hirarki yang paling populer:
- Inisialisasi: Pilih K titik secara acak sebagai centroid awal
- Assignment: Tetapkan setiap titik data ke centroid terdekat
- Update: Hitung ulang centroid dari setiap klaster
- Iterasi: Ulangi langkah 2-3 hingga centroid tidak berubah signifikan
Fungsi Objektif K-Means: \[J = \sum_{i=1}^{K} \sum_{x \in C_i} ||x - \mu_i||^2\]
di mana \(\mu_i\) adalah centroid dari klaster \(C_i\)
Kelebihan: Sederhana, efisien untuk dataset besar
Kelemahan: Memerlukan jumlah klaster (K) ditentukan sebelumnya, sensitif terhadap inisialisasi, mengasumsikan klaster berbentuk bola
Ilustrasi K-Means

Metode Elbow untuk Menentukan K
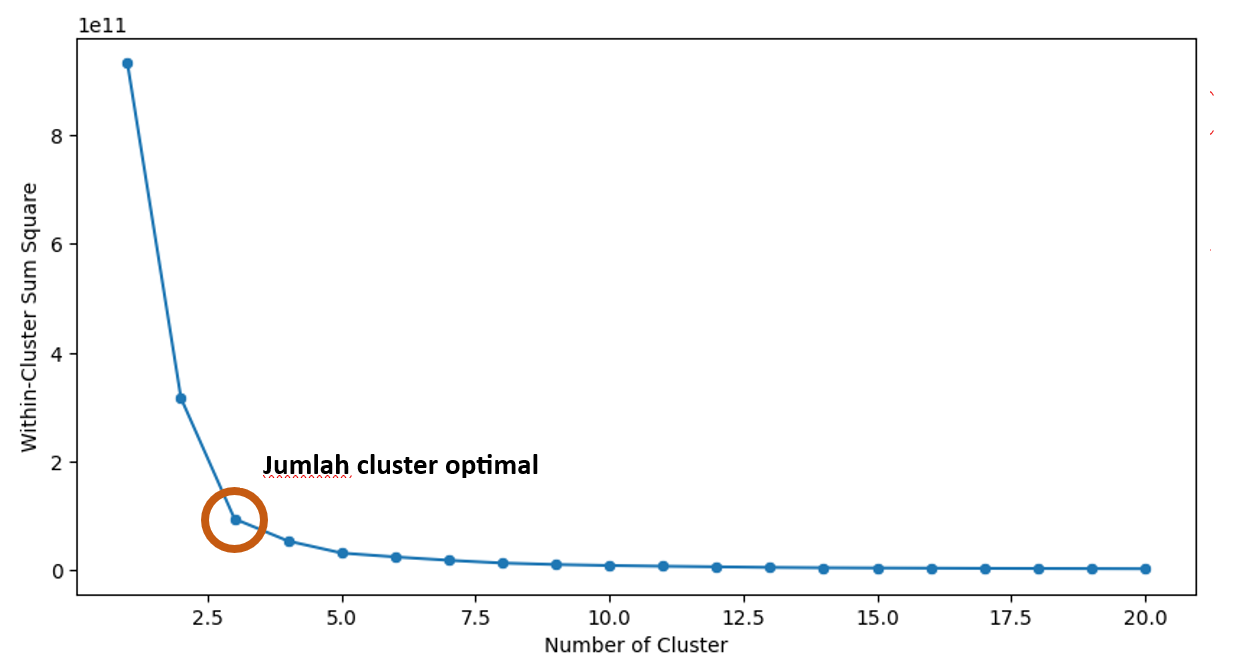
Metode Elbow membantu menentukan jumlah klaster optimal (K) dengan: (1) Menjalankan K-Means dengan berbagai nilai K (2) Menghitung Within-Cluster Sum of Squares (WCSS) untuk setiap K (3) Memilih K di “siku” grafik, di mana penambahan klaster memberikan pengurangan WCSS yang kecil
\[WCSS = \sum_{i=1}^{K} \sum_{x \in C_i} ||x - \mu_i||^2\]
Alternatif: Silhouette Score, Gap Statistic, dll.
Evaluasi Clustering
Metrik evaluasi untuk clustering:
| Metrik | Deskripsi | Rentang |
|---|---|---|
| Silhouette Coefficient | Mengukur kohesi dan separasi klaster | [-1, 1], lebih tinggi lebih baik |
| Calinski-Harabasz Index | Ratio varians antar dan dalam klaster | [0, ∞), lebih tinggi lebih baik |
| Davies-Bouldin Index | Rata-rata kesamaan antar klaster | [0, ∞), lebih rendah lebih baik |
| Dunn Index | Ratio jarak minimum antar klaster dan diameter klaster maksimum | [0, ∞), lebih tinggi lebih baik |
Implementasi dengan Scikit-Learn
# Hierarchical Clustering
from sklearn.cluster import AgglomerativeClustering
import scipy.cluster.hierarchy as sch
import matplotlib.pyplot as plt
# Membuat dendogram
plt.figure(figsize=(10, 7))
dendrogram = sch.dendrogram(sch.linkage(X, method='ward'))
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Euclidean Distance')
plt.show()
# Mengimplementasikan hierarchical clustering
hc = AgglomerativeClustering(n_clusters=4, metric='euclidean', linkage='ward')
y_hc = hc.fit_predict(X)
# K-Means Clustering
from sklearn.cluster import KMeans
# Metode Elbow
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', random_state=42)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
# Melakukan K-Means dengan jumlah cluster optimal
kmeans = KMeans(n_clusters=4, init='k-means++', random_state=42)
y_kmeans = kmeans.fit_predict(X)Perbandingan Metode Clustering
| Metode | Kelebihan | Kelemahan | Aplikasi |
|---|---|---|---|
| Hierarchical | Tidak perlu tentukan jumlah klaster di awal; Visualisasi dendogram | Komputasi mahal; Tidak praktis untuk dataset besar | Biologi, taksonomi, visualisasi hirarki |
| K-Means | Sederhana, efisien, mudah diinterpretasi | Perlu tentukan K; Sensitif terhadap inisialisasi; Asumsi bentuk klaster | Segmentasi pasar, kompresi gambar |
| DBSCAN | Menemukan klaster berbentuk kompleks; Tahan terhadap noise | Sulit menentukan parameter optimal; Masalah dengan kepadatan bervariasi | Deteksi outlier, analisis spasial |
| Gaussian Mixture | Probabilistik; Fleksibel dalam bentuk klaster | Sensitif terhadap inisialisasi; Bisa overfit | Pemodelan distribusi kompleks |
Aplikasi Clustering
Clustering memiliki banyak aplikasi praktis:
- Segmentasi Pelanggan: Mengelompokkan pelanggan berdasarkan perilaku pembelian, membantu dalam strategi pemasaran yang ditargetkan
- Analisis Gambar: Segmentasi gambar, pengenalan objek, kompresi
- Bioinformatika: Pengelompokan gen dengan pola ekspresi serupa, analisis protein
- Sistem Rekomendasi: Menemukan pengguna dengan preferensi serupa
- Analisis Dokumen: Pengelompokan dokumen terkait, pengorganisasian informasi
- Deteksi Anomali: Mengidentifikasi outlier dalam data
- Analisis Jaringan Sosial: Menemukan komunitas dalam jaringan sosial
Materi Tambahan
- Video: StatQuest - K-means clustering
- Video: Hierarchical Clustering
- Tutorial: Scikit-learn Clustering Documentation
- Interactive: Visualizing K-Means Algorithm
