
Statistika dan Probabilitas - Cookbook
Statistika deskriptif
Statistika deskriptif menyediakan ringkasan yang secara kuantitatif menggambarkan sampel data.
Populasi
Populasi mengacu pada seluruh kelompok individu yang ingin kita tarik kesimpulan tentangnya.
Sampel
Sampel mengacu pada kelompok orang (biasanya lebih kecil) yang telah kita kumpulkan datanya.

Membuat data populasi dan sampel
Untuk contoh-contoh selanjutnya, mari kita buat populasi data di R…:
Seperti apa nilai-nilainya?
Rata-rata (Mean)
Rata-rata, sering disebut juga average, didefinisikan sebagai jumlah dari semua nilai dibagi dengan banyaknya nilai. Ini adalah ukuran tendensi sentral yang memberi tahu kita apa yang terjadi di sekitar tengah data.
\(\bar{x} = \frac{1}{n} \sum_{i=i}^{n} x_{i}\)
Di R, kita menggunakan fungsi mean():
Median
Median dari sebuah dataset adalah nilai tengah ketika data diurutkan secara menaik, atau rata-rata dari dua nilai tengah jika dataset memiliki jumlah observasi genap.
\(\tilde{x} = \begin{cases} x_{(\frac{n+1}{2})} & \text{jika } n \text{ ganjil} \\ \frac{x_{(\frac{n}{2})} + x_{(\frac{n}{2}+1)}}{2} & \text{jika } n \text{ genap} \end{cases}\)
Di R, kita menggunakan fungsi median():
Modus (Mode)
Statistik modus mewakili nilai yang paling sering muncul dalam sebuah dataset.
Di R, tidak ada fungsi mode(). Sebagai gantinya, kita menghitung berapa banyak setiap nilai dan memilih yang memiliki jumlah tertinggi:
Rentang (Range)
Rentang adalah selisih antara nilai maksimum dan minimum dalam sebuah dataset.
Di R, kita dapat menggunakan fungsi max() dan min() lalu mengurangkan nilainya:
Perhatikan bahwa fungsi range() mengembalikan nilai minimum dan maksimum, bukan satu nilai:
Varians sampel
Varians sampel memberi tahu kita tentang seberapa tersebar datanya. Varians yang lebih rendah menunjukkan bahwa nilai-nilai cenderung dekat dengan rata-rata, dan varians yang lebih tinggi menunjukkan bahwa nilai-nilai tersebar di rentang yang lebih luas.
\(s^2 = \frac{\Sigma_{i= 1}^{N} (x_i - \bar{x})^2}{n-1}\)
Di R, kita menggunakan fungsi var():
Simpangan baku sampel
Simpangan baku sampel adalah akar kuadrat dari varians. Ini juga memberi tahu kita tentang seberapa tersebar datanya.
\(s = \sqrt{\frac{\Sigma_{i= 1}^{N} (x_i - \bar{x})^2}{n-1}}\)
Di R, kita menggunakan fungsi sd():
Boxplot
Boxplot (diagram kotak) adalah visualisasi yang menampilkan distribusi data berdasarkan lima nilai ringkasan: minimum, kuartil pertama (Q1), median (Q2), kuartil ketiga (Q3), dan maksimum. Titik di luar batas atas dan bawah dianggap sebagai outlier.
Interquartile Range (IQR):
\[IQR = Q_3 - Q_1\]
Batas Bawah: \[\text{Lower Fence} = Q_1 - 1.5 \times IQR\]
Batas Atas: \[\text{Upper Fence} = Q_3 + 1.5 \times IQR\]
Membuat boxplot di R:
Menghitung nilai-nilai kuartil:
Statistika deskriptif
Statistika deskriptif menyediakan ringkasan yang secara kuantitatif menggambarkan sampel data.
- Rata-rata: Jumlah nilai dibagi dengan banyaknya nilai.
- Median: Nilai tengah dari data ketika diurutkan.
- Modus: Nilai yang paling sering muncul.
- Rentang: Selisih antara nilai maksimum dan minimum.
- Varians: Rata-rata dari kuadrat selisih dari rata-rata.
- Simpangan baku: Akar kuadrat dari varians.
- Boxplot: Visualisasi distribusi data berdasarkan lima nilai ringkasan.
Latihan
5 5 3 6 7 1 6
05:00
- Hitunglah rata-rata, median, dan modus dari data di atas!
Probabilitas (Peluang)
Probabilitas adalah ukuran kemungkinan suatu peristiwa akan terjadi.
Apa itu Probabilitas?
Probabilitas menjawab pertanyaan: Seberapa mungkin sesuatu terjadi?
Contoh Sederhana:
- Peluang mendapat kepala saat melempar koin: 50%
- Peluang mendapat angka 6 saat melempar dadu: 1/6 atau ≈ 16.7%
- Peluang hujan besok: bisa 30%, 60%, atau 90% tergantung cuaca
Rumus Dasar Probabilitas
Probabilitas = (Jumlah kejadian yang diinginkan) / (Total kemungkinan kejadian)
\[P(A) = \frac{\text{Kejadian yang diinginkan}}{\text{Total kemungkinan}}\]
Contoh: Peluang mendapat angka genap (2, 4, 6) saat melempar dadu:
\[P(\text{genap}) = \frac{3}{6} = 0.5 \text{ atau } 50\%\]
Kombinatorika
Kombinatorika adalah cabang matematika yang mempelajari cara menghitung banyaknya kemungkinan atau cara mengatur objek.
Apa itu Kombinatorika?
Kombinatorika menjawab pertanyaan: Berapa banyak cara untuk mengatur atau memilih sesuatu?
Contoh Sederhana:
- Berapa banyak cara memilih 2 buah dari 5 buah apel?
- Berapa banyak cara mengatur 3 orang duduk di bangku?
- Berapa banyak password 4 digit yang bisa dibuat dari angka 0-9?
Permutasi (Pengaturan)
Permutasi adalah banyaknya cara mengatur objek di mana urutan penting.
\[P(n,r) = \frac{n!}{(n-r)!}\]
Dimana:
- \(n\) = jumlah total objek
- \(r\) = jumlah objek yang dipilih
- \(n!\) = faktorial (contoh: 5! = 5 × 4 × 3 × 2 × 1 = 120)
Contoh: Berapa banyak cara mengatur 3 orang (A, B, C) di 3 kursi?
\[P(3,3) = \frac{3!}{(3-3)!} = \frac{6}{1} = 6\]
Caranya: ABC, ACB, BAC, BCA, CAB, CBA
Kombinasi (Pemilihan)
Kombinasi adalah banyaknya cara memilih objek di mana urutan tidak penting.
\[C(n,r) = \frac{n!}{r!(n-r)!}\]
Dimana:
- \(n\) = jumlah total objek
- \(r\) = jumlah objek yang dipilih
Contoh: Berapa banyak cara memilih 2 orang dari 3 orang (A, B, C)?
\[C(3,2) = \frac{3!}{2!(3-2)!} = \frac{6}{2 \times 1} = 3\]
Caranya: AB, AC, BC (tidak sama dengan BA, CA, CB)
Perbedaan Permutasi vs Kombinasi
| Aspek | Permutasi | Kombinasi |
|---|---|---|
| Urutan | Penting | Tidak penting |
| Rumus | \(\frac{n!}{(n-r)!}\) | \(\frac{n!}{r!(n-r)!}\) |
| Contoh | ABC ≠ BAC | AB = BA |
Faktorial di R
Mari kita hitung faktorial dan permutasi/kombinasi di R:
Fungsi Bawaan di R
R menyediakan fungsi untuk menghitung permutasi dan kombinasi:
Contoh Praktis
Soal 1: Berapa banyak cara memilih 2 buah dari 5 buah apel?
Soal 2: Berapa banyak cara mengatur 4 orang untuk menjadi ketua, wakil, dan bendahara?
Soal 3: Ada 10 siswa, berapa banyak cara memilih 3 siswa untuk mewakili kelas?
Probabilitas Bersyarat
Probabilitas bersyarat adalah probabilitas suatu kejadian terjadi, dengan mengetahui bahwa kejadian lain sudah terjadi.
Apa itu Probabilitas Bersyarat?
Probabilitas bersyarat menjawab pertanyaan: Seberapa mungkin A terjadi, jika kita tahu B sudah terjadi?
Notasi: \(P(A|B)\) = Probabilitas A terjadi, JIKA B sudah terjadi
Contoh Sederhana:
- Peluang hari hujan hari ini, jika kemarin hujan
- Peluang seseorang sakit, jika dia sudah terkena virus
- Peluang lulus ujian, jika sudah belajar dengan sungguh-sungguh
Rumus Probabilitas Bersyarat
\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]
Dimana:
- \(P(A|B)\) = Probabilitas A terjadi, jika B terjadi
- \(P(A \cap B)\) = Probabilitas A dan B terjadi bersama-sama
- \(P(B)\) = Probabilitas B terjadi
Interpretasi sederhana:
- Kita fokus hanya pada kasus di mana B sudah terjadi
- Dari kasus itu, berapa banyak yang juga punya A?
Contoh 1: Dadu
Kita melempar satu dadu. Berapa peluang mendapat angka lebih dari 4, jika kita tahu hasilnya adalah angka genap?
Contoh 2: Kartu Remi
Dari satu deck kartu (52 kartu), kita ambil satu kartu. Berapa peluang kartu As, jika kita tahu kartu yang terambil adalah kartu hati?
Teorema Bayes
Teorema Bayes adalah rumus untuk menghitung probabilitas bersyarat dengan cara yang lebih sistematis. Ini membantu kita memperbarui kepercayaan kita ketika ada informasi baru.
Apa itu Teorema Bayes?
Teorema Bayes menjawab pertanyaan: Bagaimana kita memperbarui probabilitas ketika kita mendapat informasi baru?
Contoh Sederhana:
- Awalnya kita pikir ada 5% orang sakit
- Tapi orang itu tes positif untuk penyakit
- Sekarang, berapa persen kita yakin dia benar-benar sakit?
Rumus Teorema Bayes
\[P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\]
Dimana:
- \(P(A|B)\) = Probabilitas A terjadi, jika B sudah terjadi (yang kita cari)
- \(P(B|A)\) = Probabilitas B terjadi, jika A sudah terjadi
- \(P(A)\) = Probabilitas awal A (sebelum tahu B)
- \(P(B)\) = Probabilitas keseluruhan B terjadi
Terminologi:
- \(P(A)\) = Prior (apa yang kita tahu di awal)
- \(P(B|A)\) = Likelihood (bukti yang kita dapat)
- \(P(A|B)\) = Posterior (apa yang kita tahu setelah bukti)
- \(P(B)\) = Evidence (total probabilitas B terjadi)
Contoh: Tes Kesehatan
Dalam sebuah populasi:
- 5% orang mengidap penyakit tertentu
- Jika seseorang sakit, tes akan positif 99% (akurat)
- Jika seseorang sehat, tes akan negatif 95% (akurat)
Berapa peluang seseorang benar-benar sakit jika tes hasilnya positif?
Cara Alternatif: Menggunakan Tabel Kontingensi
Pendekatan ini lebih intuitif - kita bayangkan ada 10,000 orang, lalu hitung berapa banyak yang ada di setiap kategori.
Distribusi Probabilitas
Distribusi probabilitas menunjukkan semua kemungkinan nilai yang dapat diambil oleh variabel acak dan seberapa sering setiap nilai muncul.
Variabel acak: variabel yang nilainya ditentukan oleh hasil dari suatu proses acak (misalnya, hasil lemparan dadu).
Apa itu Distribusi Probabilitas?
Distribusi probabilitas menjawab pertanyaan: Jika kita mengulangi eksperimen berkali-kali, apa pola hasilnya?
Contoh Sederhana:
- Jika melempar dadu 1000 kali, berapa kali masing-masing angka muncul?
- Jika mengukur tinggi 1000 orang, bagaimana distribusinya?
- Jika melempar koin 100 kali, berapa banyak kepala yang akan muncul?
Dua Jenis Distribusi Probabilitas
1. Distribusi Diskrit (hanya nilai bulat)
- Hasil: 0, 1, 2, 3… (tidak ada nilai di antaranya)
- Contoh: jumlah koin kepala, jumlah kegagalan
2. Distribusi Kontinu (nilai desimal)
- Hasil: bisa berapa saja (1.5, 1.234, dll)
- Contoh: tinggi badan, berat badan, waktu
Distribusi Uniform
Setiap hasil memiliki peluang yang sama.
Eksperimen: Lempar dadu 600 kali
Distribusi Binomial
Distribusi Binomial menggambarkan hasil dari n percobaan independen, di mana setiap percobaan hanya memiliki dua kemungkinan hasil: sukses atau gagal. Contoh umum adalah lemparan koin sebanyak n kali, jawaban benar/salah, atau respon ya/tidak.
🎯 Eksperimen: Lempar koin 10 kali, ulangi 1000 kali
Distribusi Normal
Distribusi berbentuk lonceng, simetris di sekitar mean.
Eksperimen: Ukur tinggi 1000 orang (μ=170, σ=10)
PENTING: Y-axis = Density, bukan Probabilitas! - Probabilitas = luas area di bawah kurva
Distribusi Normal: Aturan 68-95-99.7
Dalam distribusi normal:
- 68% data berada dalam 1 SD dari mean
- 95% data berada dalam 2 SD dari mean
- 99.7% data berada dalam 3 SD dari mean
Contoh: Berapa Peluang Tinggi > 180 cm?
Distribusi Poisson
Jumlah kejadian dalam interval waktu/ruang tertentu.
Contoh: Rata-rata 5 email per jam
Distribusi Eksponensial
Waktu tunggu hingga kejadian pertama terjadi.
Contoh:
- Waktu hingga pelanggan berikutnya datang
- Waktu hingga lampu mati
- Waktu hingga email berikutnya masuk
Parameter: λ (lambda) = rata-rata kejadian per satuan waktu
Hubungan dengan Poisson:
- Poisson: Berapa banyak kejadian dalam waktu t?
- Eksponensial: Berapa lama t sampai kejadian berikutnya?
Eksponensial: Contoh Pelanggan
Skenario: Rata-rata 6 pelanggan per jam (λ = 6)
- Berapa lama menunggu pelanggan berikutnya?
Eksponensial: Perhitungan Probabilitas
Berapa peluang menunggu < 10 menit?
Distribusi Probabilitas Lainnya
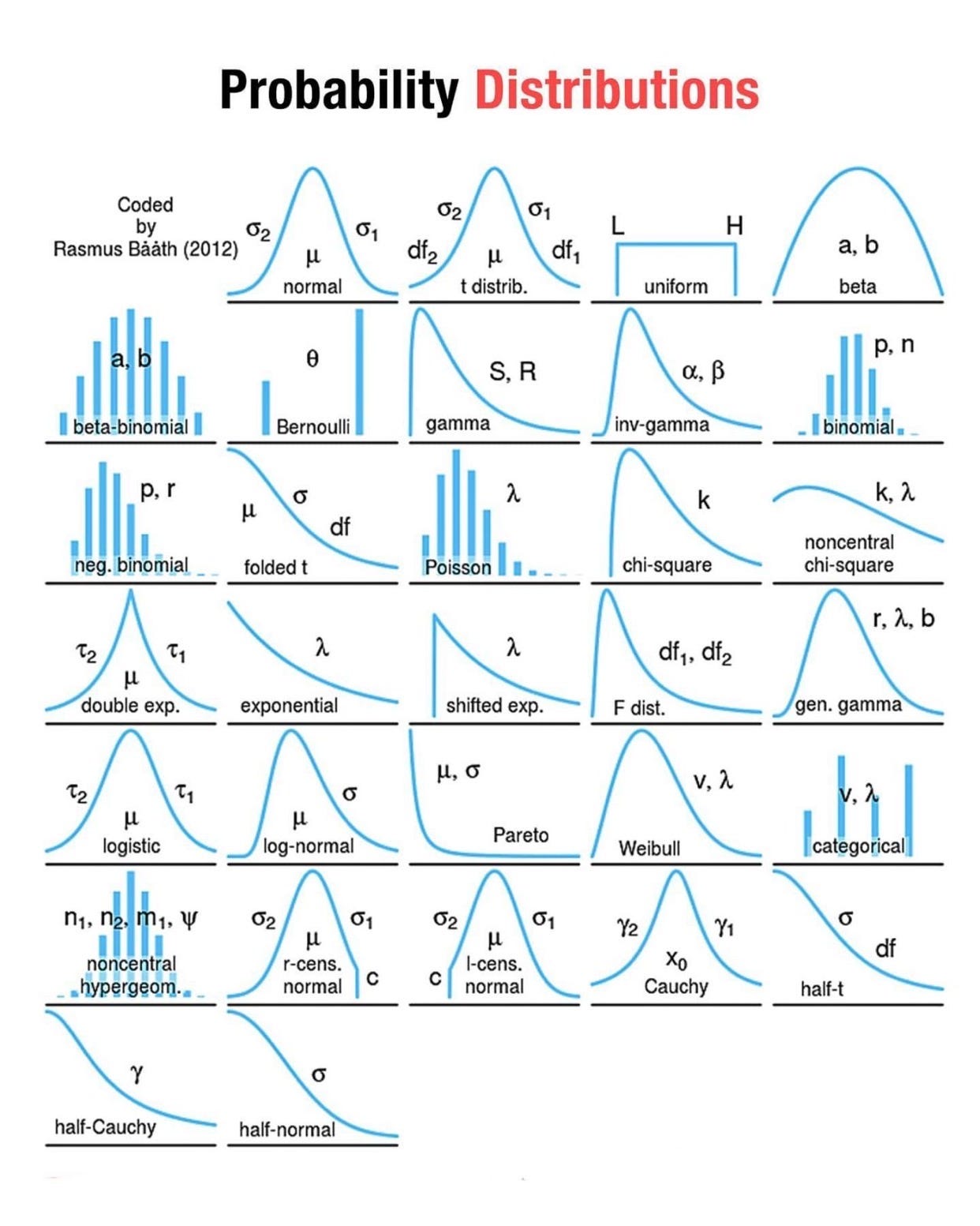
Ringkasan
| Distribusi | Jenis | Contoh |
|---|---|---|
| Uniform | Diskrit | Dadu, kartu |
| Binomial | Diskrit | Koin, ya/tidak |
| Poisson | Diskrit | Kejadian per interval |
| Normal | Kontinu | Tinggi, berat, skor |
| Eksponensial | Kontinu | Waktu antar kejadian |
Tugas
- Lakukan eksperimen sederhana tentang suatu kejadian acak (misalnya lempar koin, dadu, atau ukur sesuatu).
- Kumpulkan data dari eksperimen tersebut (minimal 50 percobaan).
- Jelaskan jenis distribusi yang sesuai dengan data yang diperoleh.
- Distribusi diskrit atau kontinu?
- Jenis distribusi apa yang paling sesuai atau mendekati?
- Kerjakan secara mandiri atau kelompok sebanyak 2 orang.
- Presentasikan hasilnya di pertemuan berikutnya.